As JavaScript applications on the web have grown more complex, so too has the complexity of dealing with state in those applications — state being the aggregate of all the data that an application needs to perform its function. Over the last several years, there has been a ton of great innovation in the realm of state management through tools like Redux, MobX, and Vuex. Something that hasn’t gotten quite as much attention, though, is state design.
What in the heck do I mean by state design?
Let’s set the scene a little bit. In the past, when building an application that needs to fetch some data from a backend service and display it to the user, I’ve designed my state to use boolean flags for various things like isLoading, isSuccess, isError, and so on down the line. As this number of boolean flags grows, though, the number of possible states that my application can have grows exponentially with it — significantly increasing the likelihood of a user encountering an unintentional or error state.
To solve this issue, I’ve spent the last several months exploring the use of finite state machines as a way to better design the state of my applications.
Finite state machines are a mathematical model of computation, initially developed in the early 1940s, that have been used for decades to build both hardware and software for a wide array of technologies.
A finite state machine can be defined as any abstract machine that exists in exactly one of a finite number of states at a given time. In more practical terms, though, a state machine is characterized by a list of states with each state defining a finite, deterministic set of states that can be transitioned to by a given action.
Due to this finite and deterministic nature, we can use state diagrams to visualize our application — before or after it’s been built.
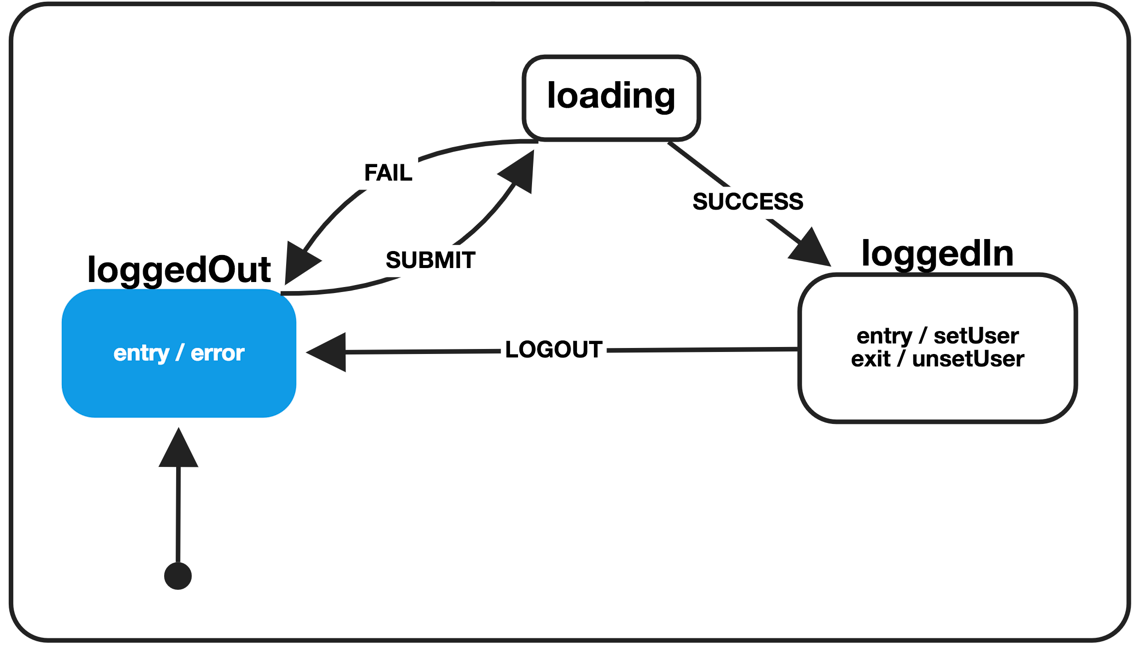
For example, if we wanted to visualize an authentication workflow, we could have three overarching states that our application could be in for a user: logged in, logged out, or loading.
State machines, owing to their predictability, are especially popular in applications where reliability is critical — such as aviation software, manufacturing, and even the NASA Space Launch System. They’ve been a mainstay in the game development community for decades, as well.
In this article, we’ll tackle building something that most applications on the web use: authentication. We’ll use the state diagram above to guide us.
Before we get started, though, let’s familiarize ourselves with some of the libraries and APIs we’ll be using to build this application.
React Context API
React 16.3 introduced a new, stable version of the Context API. If you’ve worked much with React in the past, you may be familiar with how data is passed from parent to child through props. When you have certain data that is needed by a variety of components, you can end up doing what’s known as prop drilling — passing data through multiple levels of the component tree to get the data to a component that needs it.
Context helps alleviate the pain of prop drilling by providing a way to share data between components without having to explicitly pass that data through the component tree, making it perfect for storing authentication data.
When we create context, we get a Provider and Consumer pair. The provider will act as the “smart,” stateful component that contains our state machine definition, and maintains a record of the current state of our application.
xstate
xstate is a JavaScript library for functional, stateless finite state machines and statecharts — it will provide us a nice, clean API for managing definitions and transitions through our states.
A stateless finite state machine library might sound a bit strange, but essentially what it means is that xstate only cares about the state and transition that you pass it — meaning it’s up to your application to keep track of its own current state.
xstate has a lot of features worth mentioning that we won’t cover much in this article (since we’ll only begin to scratch the surface on statecharts): hierarchical machines, parallel machines, history states, and guards, just to name a few.
The approach
So, now that we’ve had a little bit of an introduction to both Context and xstate, let’s talk about the approach we’ll be taking.
We’ll start by defining the context for our application, then creating a stateful <App /> component (our provider) that will contain our authentication state machine, along with information about the current user and a method for the user to logout.
To set the stage a bit, let’s take a quick look at a CodePen demo of what we’ll be building.
See the Pen Authentication state machine example by Jon Bellah (@jonbellah) on CodePen.
So, without further ado, let’s dig into some code!
Defining our context
The first thing we need to do is define our application context and set it up with some default values. Default values in context are helpful for allowing us to test components in isolation, since the default values are only used if there is no matching provider.
For our application, we’re going to set up a few defaults: authState which will be the authentication state of the current user, an object called user which will contain data about our user if they’re authenticated, then a logout() method that can be called anywhere in the app if the user is authenticated.
const Auth = React.createContext({ authState: 'login', logout: () => {}, user: {},
});Defining our machine
When we think about how authentication behaves in an application, in its simplest form, there are three primary states: logged out, logged in, and loading. These are the three states we diagramed earlier.
Looking back at that state diagram, our machine consists of those same three states: logged out, logged in, and loading. We also have four different action types that can be fired: SUBMIT, SUCCESS, FAIL, and LOGOUT.
We can model that behavior in code like so:
const appMachine = Machine({ initial: 'loggedOut', states: { loggedOut: { onEntry: ['error'], on: { SUBMIT: 'loading', }, }, loading: { on: { SUCCESS: 'loggedIn', FAIL: 'loggedOut', }, }, loggedIn: { onEntry: ['setUser'], onExit: ['unsetUser'], on: { LOGOUT: 'loggedOut', }, }, },
});So, we just expressed the diagram from earlier in code, but are you ready for me to let you in on a little secret? That diagram was generated from this code using David Khourshid’s xviz library — which can be used to visually explore the actual code that powers your state machines.
If you’re interested in diving deeper into complex user interfaces using finite state machines, David Khourshid has a related article here on CSS-Tricks worth checking out.
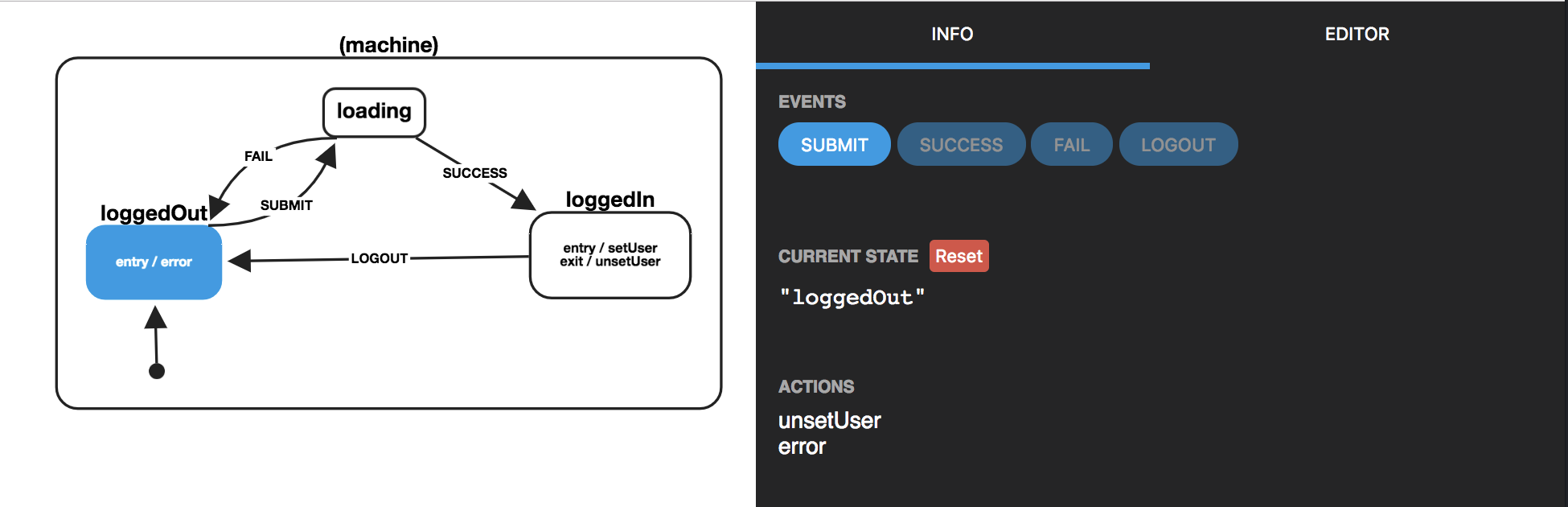
This can be an incredibly powerful tool when trying to debug problematic states in your application.
Referring back to the code above now, we define our initial application state — which we’re calling loggedOut since we’ll want to show the login screen on an initial visit.
Note that in a typical application, you’d probably want to start from the loading state and determine if the user was previously authenticated… but since we’re faking the login process, we’re starting from the logged out state.
In the states object, we define each of our states along with the corresponding actions and transitions for each of those states. Then we pass all that as an object to the Machine() function, which is imported from xstate.
Along with our loggedOut and loggedIn states, we’ve defined some actions that we want to fire when our application enters or exits those states. We’ll look at what those actions do in a bit.
This is our state machine.
To break things down one more time, let’s look at the loggedOut: { on: { SUBMIT: 'loading'} } line . This means that if our application is in the loggedOut state and we call our transition function with an action of SUBMIT, our application will always transition from the loggedOut state to the loading state. We can make that transition by calling appMachine.transition('loggedOut', 'SUBMIT').
From there, the loading state will either move the user along as an authenticated user or send them back to the login screen and display an error message.
Creating our context provider
The context provider will be the component that sits at the top level of our application and houses all the data related to an authenticated — or unauthenticated — user.
Working in the same file as our state machine definition, let’s create an <App /> component and set it up with everything we’ll need. Don’t worry, we’ll cover what each method does in just a moment.
class App extends React.Component { constructor(props) { super(props); this.state = { authState: appMachine.initialState.value, error: '', logout: e => this.logout(e), user: {}, }; } transition(event) { const nextAuthState = appMachine.transition(this.state.authState, event.type); const nextState = nextAuthState.actions.reduce( (state, action) => this.command(action, event) || state, undefined, ); this.setState({ authState: nextAuthState.value, ...nextState, }); } command(action, event) { switch (action) { case 'setUser': if (event.username) { return { user: { name: event.username } }; } break; case 'unsetUser': return { user: {}, }; case 'error': if (event.error) { return { error: event.error, }; } break; default: break; } } logout(e) { e.preventDefault(); this.transition({ type: 'LOGOUT' }); } render() { return ( <Auth.Provider value={this.state}> {this.state.error} {this.state.authState === 'loggedIn' ? ( <Dashboard /> ) : ( <Login transition={event => this.transition(event)} /> )} </div> </Auth.Provider> ); }
}Whew, that was a lot of code! Let’s break it down into manageable chunks by taking a look at each method of this class individually.
In the constructor(), we’re setting our component state to the initial state of our appMachine, as well as setting our logout function in state, so that it can be passed through our application context to any consumer that needs it.
In the transition() method, we’re doing a few important things. First, we’re passing our current application state and the event type or action to xstate, so we can determine our next state. Then, in nextState, we take any actions associated with that next state (which will be one of our onEntry or onExit actions) and run them through the command() method — then we take all of the results and set our new application state.
In the command() method, we have a switch statement that returns an object — depending on the action type — which we use to pass data into our application state. This way, once a user has authenticated, we can set relevant details about that user — username, email, id, etc. — into our context, making it available to any of our consumer components.
Finally, in our render() method, we’re actually defining our provider component and then passing all of our current state through the value props, which makes the state available to all of the components beneath it in the component tree. Then, depending on the state of our application, we’re rendering either the dashboard or the login form for the user.
In this case, we have a pretty flat component tree beneath our provider (Auth.Provider), but remember that context allows that value to be available to any component beneath our provider in the component tree, regardless of depth. So, for example, if we have a component nested three or four levels down and we want to display the current user name, we can just grab that out of context, rather than drilling it all the way down to that one component.
Creating context consumers
Now, let’s create some components that consume our application context. From these components, we can do all sorts of things.
We can start by building a login component for our application.
class Login extends Component { constructor(props) { super(props); this.state = { yourName: '', } this.handleInput = this.handleInput.bind(this); } handleInput(e) { this.setState({ yourName: e.target.value, }); } login(e) { e.preventDefault(); this.props.transition({ type: 'SUBMIT' }); setTimeout(() => { if (this.state.yourName) { return this.props.transition({ type: 'SUCCESS', username: this.state.yourName, }, () => { this.setState({ username: '' }); }); } return this.props.transition({ type: 'FAIL', error: 'Uh oh, you must enter your name!', }); }, 2000); } render() { return ( <Auth.Consumer> {({ authState }) => ( <form onSubmit={e => this.login(e)}> <label htmlFor="yourName"> <span>Your name</span> <input id="yourName" name="yourName" type="text" value={this.state.yourName} onChange={this.handleInput} /> </label> <input type="submit" value={authState === 'loading' ? 'Logging in...' : 'Login' } disabled={authState === 'loading' ? true : false} /> </form> )} </Auth.Consumer> ); }
}
Oh my! That was another big chunk of code, so let’s walk through each method again.
In the constructor(), we’re declaring our default state and binding the handleInput() method so that it references the proper this internally.
In handleInput(), we’re taking the value of our form field from our render() method and setting that value in state — this is referred to as a controlled form.
The login() method is where you would normally place your authentication logic. In the case of this app, we’re just faking a delay with setTimeout() and either authenticating the user — if they’ve provided a name — or returning an error if the field was left empty. Note that the transition() function that it calls is actually the one we defined in our <App /> component, which has been passed down via props.
Finally, our render() method displays our login form, but notice that the <Login /> component is also a context consumer. We’re using the authState context to determine whether or not to show our login button in a disabled, loading state.
Using context from deep in the component tree
Now that we’ve handled the creation of our state machine and a way for users to login to our application, we can now rely on having information about that user within any component nested under our <Dashboard /> component — since it will only ever be rendered if the user is logged in.
So let’s create a stateless component that grabs the username of the current authenticated user and displays a welcome message. Since we’re passing the logout() method to all of our consumers, we can also give the user the option of logging out from anywhere in the component tree.
const Dashboard = () => ( <Auth.Consumer> {({ user, logout }) => ( Hello {user.name} <button onClick={e => logout(e)}> Logout </button> </div> )} </Auth.Consumer>
);Building larger applications with statecharts
Using finite state machines with React doesn’t have to be limited to authentication, nor does it have to be limited to the context API.
Using statecharts, you can have hierarchical machines and/or parallel machines — meaning individual React components can have their own internal state machine, but still be connected to the overall state of your application.
In this article, we’ve primarily focused on using xstate directly with the native Context API; in larger applications, I highly recommend looking at react-automata, which provides a thin layer of abstraction over the top of xstate. react-automata has the added benefit of being able to automagically generate Jest tests for your components.
State machines and state management tools are not mutually exclusive
It’s easy to get confused by thinking you must either use, say, xstate or Redux; but it’s important to note that state machines are more of an implementation concept, concerned with how you design your state — not necessarily how you manage it.
In fact, state machines can be used with just about any un-opinionated state management tool. I encourage you to explore various approaches to determine what works best for you, your team, and your application(s).
In conclusion
These concepts can be extended to the real world without having to refactor your entire application. State machines are an excellent refactor target — meaning, next time you’re working on a component that is littered with boolean flags like isFetching and isError, consider refactoring that component to use a state machine.
As a front-end developer, I’ve found that I’m often fixing one of two categories of bugs: display-related issues or unexpected application states.
State machines make the second category virtually disappear.
If you’re interested in diving deeper into state machines, I’ve spent the last several months working on a course on finite state machines — if you sign up for the email list, you’ll receive a discount code when the course launches in August.
The post Finite State Machines with React appeared first on CSS-Tricks.




